|
|
| << PREV |
|
|
The poor world is almost 6,000 years old.
WILLIAM SHAKESPEARE
(1599)[1]
It seems that as long as mankind has been keeping records, there has been a compulsion to keep track of time, the age of the individual, of his social group, his country, his empire, and of civilization itself. The records have been chiselled in stone and kept on paper and papyrus, but it is only in the past two millennia that the Judeo-Christian West has related its records to one historical event, a fact that has greatly simplified the record keeping. Dates within the A.D. time frame are, thus, fairly certain. The further one goes back in the B.C. era, however, the dates become increasingly less certain until, eventually, beyond about 2000 B.C., the dates given are actually a consensus of opinions from the prevailing school of thought.
The archaeological dates depend on a continuum of evidence, such as interrelated king lists with the years of reign, and as such, this is primary data. Dating by the carbon 14 radiometric method, for example, is secondary data, because this method is first calibrated against archaeologically dated material. More will be said of the carbon 14 method in the next chapter.
To go back further in time, estimates are made from the natural processes,
largely independent of each other and certainly independent of the hand
of man. More will be said of these in this chapter and the next, but it
may first be asked, Can we legitimately consider the ancient written records?
There are many of these of which the Bible is only one. As in the case
of the written testimony of our own birth, these records are only as good
as our trust in the authors. Although these sources cannot be taken as
proof of the beginning, we might consider their coincidental record from
widely different cultures to be circumstantial evidence.
The Age of the Earth Before Lyell and Darwin
One concise and readily available source of nineteenth century information is Robert Young's concordance, and in the popular twenty-second edition, under "creation", will be found a list of thirty-seven computations of the date of creation from a possible list of more than one hundred and twenty. Of these thirty-seven, thirty are based on the Bible and seven are derived from other sources -- Abyssinian, Arab, Babylonian, Chinese, Egyptian, Indian, and Persian. Not one of these ancient records puts the date of creation earlier than 7000 B.C. In all the hundreds of thousands of years over which hominid man is alleged to have evolved, it is surely more than coincidental that ancient civilizations, which were by no means ignorant of timekeeping by astronomical methods, should all begin their historical record at this arbitrary date. In addition, all the myths and legends, however bizarre, speak of instant creation just a few thousand years earlier.
In almost every system of historical chronology, either the creation
of the world or the birth of Christ has been adopted as the reference point
to which all other dates are subordinate. The dating system based on the
birth of Christ will be familiar to most readers and is, in fact, used
throughout the world today for business transactions. However, in non-Christian
countries, and Israel specifically, the eras are referred to as: B.C.E.,
before the common era, and C.E., the common era. In religious communities
dating is often from the creation of the world. For example, orthodox Jews
begin their dating at 3760 B.C., while the Freemasons begin theirs at 4,000
B.C.

James Ussher, 1581-1656. A scholar proficient in a number of ancient languages, Ussher took the Scriptures quite literally and calculated the year of Creation to be 4004 B.C. (After Sir Peter Lely; National Portrait Gallery, London) |
Before the rise of science, it was usual for the church hierarchy to set forth pronouncements and deliberations on such issues as the age of the earth. Until the time of Darwin, the Old Testament Scriptures were held to be the literal truth. While the Bible does not spell out the date of creation, it was believed that this could be derived from the somewhat complicated genealogies and ages of the patriarchs. A number of scholars in the past have attempted to deduce the date of creation by this means, and a few of the more popular estimates were: Playfair, 4008 B.C.; Ussher, 4004 B.C.; Kepler, 3993 B.C.; and Lightfoot, 3928 B.C. These scholars were each proficient in a number of ancient languages, yet the fact that their dates were close but not coincident means that it is not a simple matter to establish the beginning exactly from the biblical genealogies; to this day there are men still working on this problem. Nevertheless, the date 4004 B.C. has generally been thought to be the most likely beginning point, and this has been associated with Anglican Archbishop James Ussher, although several other workers arrived at this same figure in Ussher's day. |
In 1701 the date 4004 B.C. for the year of creation was inserted as a marginal commentary in the English edition of the Great Bible by Bishop Lloyd and, by association, thus became incorporated into the dogma of the Christian church. By the time the theory of evolution came into open conflict with church dogma, almost every Bible published in the nineteenth century had Ussher's date appended to the first page, followed by sequential dates throughout to the time of the birth of Christ. As the church succumbed to the reasonings of science, these dates were quietly dropped from the Bible's beginning about 1880.
There are few texts that, when discussing the age of the earth, fail to mention Ussher's name and his date of 4004 B.C. Many of these texts add a further detail ascribed to Ussher and pinpoint the time of creation at 9 A.M. on 17 September or 9 A.M. on 23 October, depending on the authority being quoted. The facts are that this specification of the precise time of creation did not originate with Archbishop Ussher but with his contemporary, John Lightfoot, who, except for a propensity to indulge in some idle speculation, has been effectively used, particularly by geology and biology textbook writers, to discredit the Ussher date. Characteristically, not only have the details been attributed to the wrong author but careful reading shows, for example, that the 9 A.M. statement was actually taken out of context in the first place (Lightfoot 1825, 2:335 ).[2]
So much for the time of creation and the consequent age of the earth
from the biblical perspective. If this record is to be taken at all seriously,
it may be appreciated that the minimum age of the earth at this point is
about six thousand years; while allowing for possible omissions in the
genealogies, it might be a one thousand years or so older, but hardly more.
The exact figure may never be known, but the point is that this is about
a million times less than the current estimates of the age of the earth
as given by science. Quite obviously, these two estimates are poles apart
and provide the basis for diametrically opposed ideologies.
Time and Rationality in the Nineteenth Century
Historical time is unique; once passed, a moment can never be recaptured, and, without witnesses, can only be inferred from assumptions. It is no coincidence, then, that the theory of evolution, as formulated by Darwin and as we subsequently know it today, is founded on Lyell's geology. As we saw in Chapters Three and Four, Lyell's geology is, in turn, based on a device whereby traditional catastrophe became the quiet outworkings of natural processes observable today. That device was the philosophical stretching of time, from a few thousand years, implied by the biblical testimony and engraved on the nineteenth century mind, to an almost open-ended scale, reckoned today in thousands of millions of years. Lyell exploited the impossibility to recapture past events, and once having broken into this virgin ground, it then became a private preserve for his followers and had the convenience of having a sliding scale of time to fit the current theory.
Science was not very sophisticated in the early nineteenth century, and the only problem confronting the unproven assumption of the long ages proposed by Lyell was the mind-set of other scientists of the day and, of course, of the theologians, many of whom happened to be the same scientists! Nevertheless, the revolution from young earth to old earth was the snowball starting the whole avalanche that eventually changed mankind's entire Weltanschauung, or worldview.
Shortly after the time Lyell published his Principles of Geology (1830-33), men began to look for methods for determining the age of the earth that depended on natural processes rather than Archbishop Ussher's biblical interpretation. All these methods then, as today, depend on finding some chemical or physical process whose rate of activity can be measured. The product of the process is then found, and by simply dividing the product by the rate, the length of time the process has been in operation is derived. An example of this exercise was given in Chapter Four, which described the efforts in finding the age of Niagara Falls: the amount by which the Falls retreat each year is the rate of activity, and the length of the gorge is the product of the process. On paper this is straightforward enough, but in practice assumptions have to be made that are subject to the preconceptions of those carrying out the work.
Lyell's preconception of long ages caused him to modify the figure he had been given for the rate of retreat of the falls, and he finished with an age that is now conceded to have been too great. It is important, then, that whatever rate is being measured be done so accurately and without bias; this is best carried out by taking an average of the values obtained by several observers over a number of years.
The most important decision that had to be faced when calculating the
age of the earth was to agree that the measured rate of the physical process
had always been the same. In nineteenth century investigations, as well
as those today, the doctrine of uniformitarianism made it easy to assume
that the rates of these processes, that is, cutting of gorges, settling
of river sediments, etc., had been constant. In many cases this assumption
was later concluded to have been quite wrong. But the ages that were derived
at the time were held to be scientific fact, and, although this was unintended,
actually served well to undermine the biblical catastrophists' beliefs
of a few thousand years; these figures played a vital part in establishing
the theory of evolution.
Some Former Facts of Science
It was recognized quite early that rivers carried a sediment that settled
to the bottom when the water moved less rapidly, such as at points where
the river entered the ocean or at times when the river was spread out in
a flood plain. Many efforts were made to measure the sediment carried by
river water each year and then measure the total quantity of sediment deposited
at the river mouth. It was always assumed that the rate of deposition of
sediment had been constant. While there were some uncertainties in measurement,
in the 1850s there came a unique opportunity to measure both the rate of
sedimentation and the total deposit at the same location and with some
precision. Napoleon's popularization of the wonders of ancient Egypt brought
the realization that the River Nile flooded the fertile valley every year
and left a thin deposit of mud. The foundation of the colossal statue of
Ramses II had been built on this deposit in the valley at Memphis and over
the ensuing years had been covered by a further nine feet of river-laid
sediment (Bonomi 1847; Lepsius 1849). When the hieroglyphics had been deciphered
and the chronology worked out, it was established that the statue had stood
for 3,200 years, so that with nine feet of deposit over this period, the
deposition rate was three-and-a-half inches per century at this point (Dunbar
1960, 18).[3] Further
excavations in the Nile valley showed that the sediment was as much as
seventy-two-feet deep in some places, but it was realized that the test
hole now extended several feet below the level of the Mediterranean
Sea, and further boring was discontinued (Lyell 1914, 29).[4]
However, at the measured rate of three-and-a-half inches per century, this
gave a maximum age of only 30,000 years, which was woefully short of the
millions of years required for Lyell's geology. The borehole project, carried
out between 1851 and 1858, became something of an embarrassment and was
discontinued. However, there is an interesting observation that was passed
over at the time and, so far as is known, has not been made since. The
rates of sediment deposition at Memphis, or at any other location where
it has been measured, can always have been greater but never very much
less. At Memphis, in order to fit Lyell's geology of, for example, only
one million years, the sediment deposited would be less than a thousandth
of an inch per century. The most fastidious housewife knows that house
dust accumulates at a greater rate than this! On the other hand, to fit
Ussher's chronology, one or two large inundations of sediment prior to
the erection of the statue would be all that was required. For instance,
if catastrophes such as volcanic eruption with great quantities of ash
are admitted, then any sedimentation rate in the past can have been very
much greater and have had the effect of shortening the calculated life
immensely.
Salt in the Sea
Another early attempt to measure the age of the earth was carried out
by John Joly, in 1899, and was based on the amount of sodium chloride (common
salt) in the oceans. Joly (1901, 247) assumed that the primitive ocean
began as pure water and that the present rate of salt addition from the
world's rivers had always been the same. Since the salinity of the world's
oceans is nearly uniform and map measurements indicate the total volume
of water, Joly, consequently, determined the number of tons of salt contained
in the oceans. Measurements at the mouths of all the world's major rivers
then showed how many tons of salt entered the oceans each year, and by
a simple division of the numbers, Joly arrived at 100 million years as
the age for the earth. At that date, Darwin's followers reluctantly accepted
this figure, and it became a scientific fact. But just in the nick of time,
it seems, radiometric methods superseded all the other methods, and estimates
of the age of the earth increased by leaps and bounds (Joly 1922).[5]
For the next half century, a number of very vague reasons were advanced
to explain away Joly's estimate based on the ocean's salt content, but
the method was, in a sense, too good and allowed little room for argument.
The original assumptions could not really be called into question, because
to do so would only shorten the age. In fact, once it was admitted that
the original ocean contained any salt at all, then it became anybody's
guess, and the catastrophist could equally well claim that the ocean had
been created salty in the first place, only a few thousand years ago. At
the time Joly was working on his salt method using the world's rivers and
oceans, someone must surely have thought of the simpler approach based
on the same principle but confining the work in terms of effort and certainty
to Israel's Dead Sea.
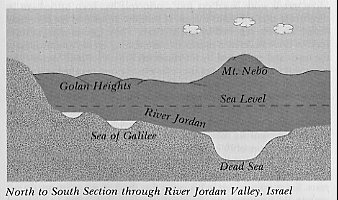
Israel's chronometer. Located 1,200 feet below sea level, the water of the Dead Sea can only leave the basin by evaporation. The salts remain and concentrate. The parameters of this system are accurately known and indicate only a few thousand years for its existence. (Author) |
Israel's Chronometer
Geologically, the Dead Sea Valley is part of a rift valley system that extends down through the Red Sea into the Afar region of northeastern Ethiopia. Textbook authorities maintain that the system was formed several million years go. For example, radiometric methods applied to the strata of the Afar region, where Donald Johanson discovered the now famous "Lucy", indicate that this geological formation was formed at least three million years ago (Johanson and Edey 1981, 187). At the other end of this rift valley in Israel is a water system consisting of the Sea of Galilee, the River Jordan and the Dead Sea, which are all below sea level and form a unique chronometer at the lowest point on earth. Fresh water from the Sea of Galilee flows continually into the Dead Sea via the River Jordan, while the only outlet for the Dead Sea is by evaporation; evaporated water contains no salt. Long ago the system came to equilibrium when the rate at which the water entered the Dead Sea exactly equaled the rate at which it left by evaporation, and the salts then began to concentrate.[6] |
Fortunately for the armchair investigator, all the essential data concerning
the rate at which salts concentrate in the Dead Sea have been published
and conveniently may be found in the fourteenth edition of the Encyclopaedia
Britannica:
The Dead Sea, which covers an area of 394 square miles, contains approximately 11,600,000,000 tons of salt, and the river Jordan which contains only 35 parts of salt per 100,000 of water, adds each year 850,000 tons of salt to this total (Encyclopaedia Britannica 1973, 19:995).
By simply dividing the total quantity of salt by the annual rate
of addition, the age of this geological feature is found to be a mere thirteen
thousand years, which is a far cry from the three million years claimed
for the other end of the rift valley. However, this is not all, since the
same encyclopaedia (under "salt") also points out that there are salt water
springs at the bottom of the Dead Sea and other streams that contribute
salts, so that the overall effect is to reduce the age still further. It
would be spurious to argue that the waters of the Jordan contained less
salt in the past, because the enormous lengths of time demanded by geology
would require a purity of Jordan water far greater than that of distilled
water, and this is clearly not credible.
It is reasonable to suppose that others must have drawn these same conclusions
on the Dead Sea years ago, when the waters were first analyzed, but by
that time the orthodox geological dogma prevailed, and, so far as is known,
this obvious conclusion has never been committed to print.
More Salts in the Sea
More recent work based on Joly's principle has been carried out by measuring
uranium salts instead of sodium chloride in the rivers and oceans and was
reported by Koczy (1954). These figures were, in turn, used by Cook to
derive a statement commenting on the youthfulness of the earth and published
by the respected British journal Nature. The statement was, however,
not immediately obvious, couched as it was in the cryptic terms of the
scientist. Cook (1957) concluded his article on radiogenic helium with
the remark that his results were "in approximate agreement with the chronometry
one obtains from the annual uranium flux in river water (1010
to 1011 gm/yr) compared with the total uranium present in the
oceans (about 1015 gm)" (Cook 1957, 213). Taking the figure
of 1011 as the rate at which uranium enters the oceans
and 1015 as the total product (the units may be neglected),
the age is given simply by subtracting eleven from fifteen; that is, 104
or 10,000 years. Koczy pointed out in his paper that the deep sea sediments
do not contain the enormous quantities of uranium that might be expected
and leaves the reader with some vague assumptions to account for the "missing"
uranium.[7]
| All those who conducted the river water analysis, including the
U.S. geological survey, cannot have committed a million-fold error, and
if the 10,000 years is anywhere near correct, then it begins to look as
if the original ocean contained about as much sodium chloride as it does
today but contained no uranium salts. Boldly stated, this conclusion, drawn
from the published data, runs counter to the uniformitarian dogma and would
rarely be found within the pages of the professional journals and never
in the popular press.
Back to Discarded Myths Before leaving the subject of salt in the oceans, it should be noted that it was shortly after Joly had published his early work that A.B. Macallam, in 1903, stated that there was a causal relationship between the salinity of the sea and the salt content of blood plasma. This was said to be a direct reflection of our ancient emergence from the sea, and until it was refuted a few years later, this became another scientific fact supporting the theory of evolution (Macallam 1903).[8] |

A Greek myth tells us that the love goddess Aphrodite, otherwise known as Venus or Cytherea, was born from the sea. Aphrodite means "foam-born". Does this Greek wisdom hint that mankind too was born from the sea, as in the textbook explanations we are given today? (Drawn by Mary Wardlaw) |
Cooling of the Earth and Lord Kelvin
One final method, involving the measurement of rate and product, concerned
the cooling of the earth from an assumed hot liquid state. This method
is worth mentioning here, for some of the details will be referred to in
the following chapter. The Industrial Revolution had created a great need
for coal to generate steam power. As coal mines were driven deeper, it
was noticed that the temperature rose about 1°C for every thirty meters
(one hundred feet), and it was realized that at this rate the earth must
be white hot for the greater part of its core and only cool enough to support
life on a thin outer shell. One of the nineteenth century theories for
the origin of the earth was that given authority by the French mathematician
Laplace, who proposed that our solar system began as a spinning blob of
white-hot matter. Several small pieces then became detached, continuing
to spin in the same direction and, under their own gravitational fields,
formed spheroids orbiting the central mass. The spheroids cooled to become
the planets, one of which was our earth. Although this entire scenario
has been left in the mind of the general public even to this day, as we
shall see, it was in fact refuted long ago.[9]

William Thomson, better known as Lord Kelvin, 1824-1907. A truly great scientist of the nineteenth century by whom we benefit today, his name has been overshadowed in the popular press by that of Darwin. Shown here with his compass. (Photograph by J. Annan, 1902; The Royal Photographic Society) |
Shortly after Darwin published the Origin, William Thomson (1865), afterwards Lord Kelvin, began to calculate the age of the earth assuming it had originated as Laplace had described it. Kelvin took for his datum points the time at which the surface layer crusted over (freezing point of molten rock) and the rate of heat flow through the surface of the earth as found in the coal mines. In an elegantly simple two-page paper, he effectively demolished Lyell's uniformitarian assumptions and left Darwin's theory without a foundation (Thomson 1865). Kelvin showed that the age of the earth, based on the assumption that it had cooled, was a maximum of 400 million years, while an appeal to any greater length of time would leave the earth too cold today to support life. This upper limit was too short a time for Darwin, but Kelvin's scientific stature and mathematical demonstration could not be faulted (F. Darwin and Seward 1903, 2:163).[10] Ironically, this very argument was later misinterpreted by some of the clergy, who mistook Kelvin's defense of the Christian faith (by refutation of uniformitarianism) as an advocacy of an old earth. In this way some were weaned away from the Christian dogma of a young earth towards accepting an old-earth view and, eventually, the idea of evolution itself. |
During the Kelvin-Darwinian debate over the age of the earth, nicely documented by Burchfield (1975), the Darwinians were set back by two astronomical discoveries, given relief by the death of Kelvin in 1907, finally taking the victory from the phenomenon of radioactivity that had been discovered a few years earlier. By observing the movement of sun spots, it was evident to astronomers that the sun was not spinning on its axis at the rate that would be expected from the Laplace theory; more devastating was the discovery that some planets revolved in a forward direction about their axis and others in a retrograde direction (see note 9). According to the theory, they should all revolve in the same direction. This effectively discredited the Laplace nebular hypothesis, although, after more than a century and without a better theory to offer, the modern theory is essentially the same except for the name.
The textbook explanation today for the origin of the solar system proposes that in a process called accretion, finely dispersed gases and dust were rotating and concentrating under gravitational forces. From the fiery ball of gas generated by this process, it is then said that a disc of gas was thrown off, condensing to form the planets and eventually cooling from liquid to solid. Darwin's theory was successfully rescued from the difficulties with Lord Kelvin and the astronomers by two brilliant assumptions based on Becquerel's accidental discovery of radioactivity in 1895.
First, it was observed that radioactive decay produced a small quantity of heat, and this fact was then called on to explain the sustained high temperature of the earth's core. Having broken through Kelvin's upper limit of 400 million years, an age of more than ten times this figure is today claimed for the earth; it should be remembered, however, that this is supported entirely on the assumption that an enormous and virtually inexhaustible source of heat resides in the radioactive elements within the earth. This assumption is seldom questioned, but Ingersoll (1954) and his coworkers pointed out more than three decades ago that by reworking Kelvin's cooling data the age of the earth was shown to be 22 million years without radioactivity (Kelvin's minimum value based on Laplace's theory was 20 million years), but including the known radioactivity in the earth, the age could not exceed 45 million years (Ingersoll et al. 1954, 99). Clearly something is radically wrong, since this is but 1 percent of that required by today's biological evolution.
The second assumption was concerned with the rate of radioactive decay. An early discovered property of this decay process was that it appeared to be constant and seemingly unaffected by chemical changes, extreme heat, or pressure. The appearance of a constant decay rate was quickly assumed to be a fact, and radioactive decay was seen to be a unique and independent way to determine the age of the earth. Sir George Darwin, son of Charles Darwin, made this suggestion at the British Association meeting of 1905. By 1910 a method had been worked out and an age of 600-700 million years for a Precambrian rock mineral reported (Strutt 1910). This is modest by today's standard, but it did serve nicely as the second arm of attack on Kelvin's formidable 400-million-year barrier. Moreover, there was no likelihood of the figures being challenged since Kelvin had died three years earlier.
When these radiometric techniques were first introduced, many workers were skeptical, but as the expectation of geological ages seemed to be confirmed, the method became established and eventually swept aside all the earlier methods. It was at this point that the estimates of the age of the earth began to increase most dramatically. Engel, writing in 1969, showed that the textbook age of the earth has increased by a factor of almost one hundred since 1900, the accepted "age" then being 50 million years, while today it is claimed to be 4.6 billion, that is, 4.6 thousand, million years (see Appendix B).
The entire edifice of the old-earth model depends almost exclusively on the results given by the radiometric methods, while these, in turn, depend on the validity of certain assumptions. Textbooks tend to gloss over these assumptions, but an understanding of what is actually being assumed is essential in order to make an intelligent assessment of the method's credibility. For this reason, an attempt will be made in the remainder of this chapter and the first half of the next to patiently untie, rather than to cut, the radiometric Gordian knot.
Since these pages may appear as parched desert to the non-technical
reader they may care to take the direct flight and continue at subsection
Evidence
That Demands a Verdict in Chapter 12. The essence of what will be said
is that radioactive decay of certain elements, some of which are confined
to the rocks while others form part of every living thing, is analogous
to the old-fashioned hour-glass. The radioactive element is like the sand
in the upper glass and as it decays to become the non-radioactive element,
this material falls through into the lower glass. The method of finding
when the hour-glass was started, that is the age, consists of determining
the total amount of element in each half of the glass and measuring the
rate at which it falls from the upper vessel to the lower. The smaller
the quantity of radioactive material that remains relative to the non-radioactive
material with which it is associated, the greater is the age of the sample.
Principles of Radiometric Measurement
The alchemists of the Middle Ages believed it was possible to transmute, or change, a heavy base metal, such as iron, into the heavier noble metal, gold, and thereby make a fortune. Modern science has shown that this is generally quite impossible, but there are naturally occurring processes in which transmutation takes place spontaneously in the reverse direction, whereby unstable elements change atom by atom to form lighter stable elements. This process is known as radioactive decay and, depending on the elements involved, may take the form of alpha decay, typically producing helium gas, or beta decay, where an electron is emitted, or decay by an electron capture mechanism. The characteristic that makes the radiometric methods so valuable is the decay process, which is believed to be constant, unaffected by temperature, pressure, or, indeed, the chemical form taken by the unstable element in its initial state.
The decay process is seen as a unique kind of clock which, having begun,
has been running with unerring accuracy ever since. The underlying principle
for all the radiometric methods is that once the rate of decay for the
particular radioactive process is known, then the age of anything that
contains within it such a process may be found simply by measuring the
quantity of unstable element remaining and the associated quantity of stable
element that has accumulated to this point. These elements are usually
referred to as "parent" and "daughter" elements, respectively, and a simple
calculation using this data then gives the time the decay process has been
in operation.
The Radiometric Methods
The earliest radiometric method resulted from an observation made by Boltwood in 1907 that uranium and thorium minerals both decay radioactively to form lead and helium gas. The uranium/lead method, though limited to uranium-containing minerals, was used for many years and depends on the decay of uranium 238 to lead 206, through a complex process involving fourteen stages. Details of these stages are not essential to the present context and may be found in Appendix C. The numbers 238 and 206 refer to the atomic mass, or weight, and identify the specific isotope, or variety of the individual elements. Details of the uranium/lead method will be used to illustrate the next section.
Subsequently, other radioactive processes were found, such as the decay
of potassium minerals into argon gas or rubidium minerals into strontium,
and since rocks containing these elements as minerals are more abundant,
these methods are now the most commonly used to date rock strata. In this
way, absolute ages have been attached to the various parts of the geologic
column and its associated fossil forms. The popular carbon 14 method, which
depends on the radioactive decay of an unstable isotope of carbon, is somewhat
different from the other radiometric methods and will be discussed in the
next chapter.
Rate of Decay
Radioactive decay has always been assumed to be a constant process, occurring by random transmutation of the individual atoms of the unstable element. Some atoms will last only a few minutes before decay, while adjacent atoms will remain for thousands of years. No one can know when an individual atom will decay, and, for that matter, no one is sure why they decay. When a large number of atoms is involved, however, there is a certain statistical certainty that, at any given moment, a specific number of atoms will be in process of spontaneous change or decay. Details of these numbers give the vital rate of decay, but this is based on the assumption that it is a random process. During the past decade or so, statistical work carried out by Anderson and Spangler (1973)[11] has shown that, in fact, the decay process is not random; this means, however, that the decay rate cannot be known with certainty, putting all radiometric dating into serious question (Anderson 1972).[12] Not surprisingly, even though holding responsible scientific positions, these authors admitted to difficulty in getting their work published and since then have confessed that it has been "disregarded, discounted, disbelieved ... by virtually the entire scientific community" (Anderson and Spangler 1974).[13]
Nevertheless, the rest of the scientific fraternity remain steadfast in their belief that the rates of atomic decay have been forever constant. Accordingly, once the rates of decay of the radioactive isotopes have been determined and published, redetermination from time to time is not warranted. Indeed, the very term "decay constant" would not encourage such a practice.
In the case of the uranium 238, the decay rate and corresponding constant was settled more than half a century ago. The method consisted of taking a small crystal of the uranium-containing mineral, either zircon or, less commonly, uraninite, and, by means of a Geiger counter counting the number of alpha particles given off over a measured period of time, usually two or three days. By simple arithmetic this is reduced to a rate of so many counts per milligram of sample per hour. The rate of decay is then expressed mathematically from this information as the decay constant, or as the more familiar half-life (these terms and their mathematical relationships are explained in note 14).[14] The half-life is a convenient way of expressing the life of a process that is, theoretically, never complete and states the time required for the quantity of the "parent" material, uranium 238, to decrease by half. The half-life of uranium 238 has been reckoned as 4.51 billion years, which means if a sample began with one hundred atoms of uranium then, after one half-life, only fifty atoms of uranium are left; after two half-lives, twenty-five atoms remain, and so on. After five half-lives, or 23 billion years, only three atoms are left -- that is, the decay process is 97 percent complete. It is purely coincidental that the half-life of uranium 238 happens to be the current estimate for the age of the earth.
The number of alpha particles emitted per hour depends on the number of uranium atoms in process of decay, that is, upon the size of the sample, and for this reason the rate is expressed as "per milligram". However, the rate of emission will decrease slowly with time as the number of uranium atoms diminish but, of course, the time spans are so long that this has never been observed. In other words, the only measurements made have been in this century, while during the two-or three-day test period, the rate naturally appears uniform. The mathematical treatment of the rate to produce the decay constant, or the related half-life, removes the effect of the decreasing "parent" element. It is, then, assumed that the decay constant has, in fact, been constant throughout the entire age of the cluster of uranium atoms in the sample. This is the most important assumption and is based on the observation that the number of counts per milligram per hour appears constant, whether it was measured in the 1950s or the 1980s or from one sample to the next; moreover, neither heat nor pressure nor a number of other conditions imposed on radioactive materials seem to change this rate. It should be borne in mind that the assumption of constancy is a large step of faith, based on observations made over a few years and believed to apply to a process taking billions of years.
It was pointed out in the section on principles that as the "parent"
material steadily decreases, the "daughter" product, lead 206, correspondingly
increases. The greater the proportion of lead 206 to uranium 238, the greater
the age of the sample. However, the age can appear to be much greater than
is actually the case when the rock contained lead in its initial stages
of formation. We will examine the problem of initial lead "contamination"
in the next section.
The Initial Formation of the Mineral
In spite of the fact that the Laplace Nebular Theory was discredited many years ago, the modern accretion theory still holds to the assumption that the earth was at one time liquid and cooled slowly to produce a hard crust. Astronomy does not usually emphasize this aspect but it is quite essential for modern geology. Enormous lengths of time are then assumed, during which it is further assumed that erosion removed the top surface of all the original crustal material and redeposited it as the sedimentary (layered) rocks. In addition, there are some igneous rocks produced by hot liquid magma that has exuded to the surface from deep within the earth. It is usually only this latter type of rock, typified by the granites that have crystallized from the liquid, that is used for radiometric dating, while the age measured is from the moment the crystals were formed. This does not give the age of the earth directly because this is not the original crustal material, but this intrusive crystallized rock is useful to give the age of an associated sedimentary rock layer and, particularly, the fossils contained within it.
In cooling from the liquid to the solid state, there are definite rules
that the rapidly moving mixture of atoms obey as they find their places
in the crystal lattices of the solid material. In the mineral zircon, which
is used for this method of radiometric dating, clusters of uranium atoms
associate themselves with zircon atoms to become part of the crystal lattice.
From the moment the lattice is formed, the uranium atoms continue to decay
into lead atoms, but, in contrast to the liquid state, these now remain
fixed within the lattice in association with the "parent" uranium. The
proportion of lead 206 atoms produced in situ relative to the uranium
238 in the same lattice then gives a measure of the time since the crystal
was formed. Now all this is straightforward enough, assuming that there
has been no "contamination" of the crystal by the introduction of lead
206 at the time the crystal was being formed from the liquid. In fact,
this very thing has often happened, which gives the impression that the
crystal is much older than it really is. It may be appreciated, then, that
it is important to know how much lead 206 was included in the lattice in
the first place in order to find out how much lead 206 was produced later
by the uranium 238 decay.
Complications by Lead 206 Contamination
It may be asked how it is possible to know what the original lead content was untold millions of years ago. Aston, in 1929, discovered that there are four isotopes, or virtually identical varieties, of lead. Of these four, one form is lead 204, which is not a product of radio decay, and another is lead 206, which is radiogenic and the ultimate "daughter" of uranium 238. The contaminating lead that found its way into the crystal as it was growing from the liquid is assumed to consist of a mixture of lead 204 and lead 206 in a certain proportion. By good fortune, the mineral zircon is often associated with the nonradioactive minerals feldspar and galena, which contain lead but not uranium, and the assumption is made that the proportion of lead 204 to lead 206 found in the feldspar is the same as the proportion that "contaminated" the zircon crystal. It is reasonably assumed that the two minerals were formed at the same time, while the quantity of lead 204 does not change in either. By finding this proportion of leads in the feldspar and knowing the total lead 204 and 206 in the zircon, it is a simple matter to find the initial quantity of lead 206 and subtract this from the total to leave that which was produced in situ by decay, and so find the age of the crystal (Nier 1939).
Having made this correction with its attendant assumptions for the initial lead "contamination", it is further assumed that since the decay process began, no "parent" and no "daughter" elements have been lost or added to the crystal lattice from outside sources. For this reason, precautions are taken to ensure that the crystal originates from deep within a rock mass so that ground water cannot have transported either uranium or lead atoms in or out of the crystal lattice since it was formed. The laboratory air, for example, must be lead free -- that is, with no automotive fumes, which would cause sample contamination.
Finally, the analytical work is carried out on a selected small crystal of zircon or uraninite, while the proportions of uranium 238 and leads 204 and 206 are found by mass spectrometer techniques. The ages given by the uranium/lead method are very long running, from hundreds of millions to billions of years, but none so far approach the assumed age of the earth.[15]
One item of interest will be appropriate here concerning the current
estimate for the age of the earth. In 1956 Holmes noted that the older
the feldspar, according to the age given by the associated zircon, the
less lead 206 there was in the mixture of leads 204 and 206. It was argued
that the lead 204 had been associated with uranium, somewhere in the depths
of the earth, before it was deposited at a later time in the zircon and
feldspar crystals. By extrapolating backward in time, to the point where
there was no radioactively produced lead 206 in the lead 204 mixture, Holmes
(1956) obtained the time when he believed the earth first became crusted
over. That time was 4.5 billion years ago.
The Potassium-Argon Method of Dating
One of the drawbacks of the uranium/lead method is that the uranium-containing minerals are not too common. Potassium is one of the most common elements found in rocks, and by 1948 Aldrich and Nier had worked out a method that depended on the radioactive decay of the isotope potassium 40 into the gas argon 40. The half-life of potassium 40 has been determined as 1,310 million years, which means that the age range capable of being dated by this method tends to be less than that of the uranium/lead method and varies between 200 million and 1,600 million years. The principles, assumptions, and many of the details involved in this method are virtually the same as those described for the uranium/lead method. Once the rate of decay of potassium 40 is known, it is only necessary to determine the proportions of "parent" potassium 40 to "daughter" argon 40 for the age to be found; the more argon 40 present, the greater is the age of the sample (further details of the method will be found in Dalrymple and Lanphere 1969).
The initial formation of the potassium-containing minerals by crystallization is similar, in principle, to the formation of zircon mineral. Once the radioactive potassium 40 becomes locked into the crystal lattice, it produces argon 40 in situ, but since this is a gas, there are always the questions of whether it leaks out indicating a younger age than is actually the case, or whether it can diffuse in either from adjacent rocks or from the atmosphere indicating a greater age. There is a further question relating to argon 40 trapped in the crystal as it was formed. If it is present and not taken into account, it would give the appearance of a much greater age. There is admitted to be some guesswork involved in determining the initial argon content, and it is generally assumed that because of argon's chemical inertness, no argon is incorporated into the crystal structure when cooling from, for example, a magma (molten rock). In answer to the first question, an unexpected discovery was made in 1956, when it was shown that the then popular potassium feldspars retain only about 75 percent of the argon 40 that is generated within them. Since that date, investigators have used the potassium-containing mineral, biotite, for the igneous rocks and glauconite for the sedimentary rocks; it is assumed that all the argon 40 is retained in these minerals (Knopf 1957, 232).
The second and third questions relate to the "contamination" problem. Routine corrections are made during analysis to eliminate the possible effects of initial argon contamination from the atmosphere. It turns out that the atmosphere contains about 1 percent argon, and of that, one part is the isotope argon 36, and 295.5 parts are argon 40. It is assumed that this ratio has always been the same, so that any argon 40 trapped from the atmosphere during crystallization can be found by measuring the argon 36 and multiplying by 295.5. This value for argon 40 by contamination is deducted from the total argon 40 to give that produced by radioactive decay. The fact that corrections are made indicates that recognition is given to contamination having taken place. However, the assumption that the ratio of 1:295.5 has been constant for all time is very questionable, because argon 36 is produced in the upper atmosphere by cosmic bombardment (Rosen 1968).[16] This means that the ratio was greater in the past and has been decreasing. Therefore, a greater correction would be necessary, resulting in the samples being much younger than they now appear.
Some of the reported ages for lava rocks from Hawaii, known to be less
than 200 years old, have been given as 22 million years by the potassium/argon
method; however, this is now known to be caused by initial argon 40 contamination
during the crystal formation and can be corrected for by the method described
above (Noble and Naughton 1968; Funkhouser and Naughton 1968).[17]
It has also been found that submarine lavas contain an excess of argon
40. Interestingly, the greater the depth at which the lava was formed,
the greater the amount of argon 40 contamination giving the false impression
of a greater age (Dalrymple and Moore 1968). The pressure of sea water
has seemingly "forced" more argon 40 into the molten rock during crystallization.
Taking these facts together, an intriguing possibility presents itself:
Accepting the Creation view of a worldwide flood only a few thousand years
ago and when the argon 36 was absent or negligible, liquid magmas, crystallizing
under a mile or two of sea water, would be expected to retain a rather
high proportion of argon 40, quite indistinguishable from that subsequently
produced by radioactive decay. Such material would appear to be of extremely
great age, whereas it would, in fact, have been formed only a few thousand
years ago.
Are the Radiometric Methods Reliable?
The two most popular radiometric methods have been described in these pages, but there are other methods, such as the rubidium/strontium, and thorium/lead, the lead 207/lead 206, and the uranium 235/lead 207, which are extensively used. These last three methods involving lead are directly related to the uranium 238/lead 206 method (see Appendix C) already described and are usually carried out at the same time. The hope is that the results from the various decay processes operating within the same sample will provide confirmation or concordance; usually there is 20-30 percent discordance in results, and a decision has to be made regarding which one to report. It is assumed that the discordance is caused by lead leakage from the mineral after it has crystallized; it may be observed that, of only two possibilities, selective lead leakage is more credible than selective lead addition. However, there is really no proof for either the one assumption or the other.
Concordance of another type is claimed from deep-sea drill cores. In this case the oxygen 18 isotope method is used, by which it is found that the absolute dates -- at least those reported -- are roughly the same from core to core and line up sequentially, with the most recent dates at the top and the most ancient at the bottom. However, occasionally a whole series of results will be discordant by 30 percent or more, which does not give great cause for alarm so long as the ages are thought to be in terms of millions of years (Emiliani 1958).[18]
The half-lives, or mathematically related decay constants of the various decay processes, vary enormously from fractions of a second to millions of years, as will be evident from the table of values for the uranium/lead system in Appendix C. They are all said to be generally repeatable in the laboratory with a reasonable degree of accuracy, though there is still disagreement over some values; the potassium 40 half-life, for example, is still within a few percentage points of agreement (Dalrymple and Lanphere 1969, 41).
Radiometric ages determined after about 1950 tend to be considered more reliable than earlier estimates for three reasons: first, the methods became more popular about that time, and with greater usage the equipment and techniques became more sophisticated. Second, partially concordant results began to be obtained from independent decay processes occurring simultaneously within the same sample. Third, as data accumulated and were published, researchers began to have expectations of results, and a tendency developed to report only those results that fit the expectations. This has become the normal practice, but the overall effect does tend to build up a false measure of confidence in the method.
When it is recalled that these radiometric methods are based on a series
of similar assumptions, it is perhaps not too surprising that some concordance,
or partial concordance, of results would occur. It will be useful at this
point to see what has been said about these assumptions.
The Assumptions of Radiometric Dating
To recapitulate what has been said regarding the major assumptions on which the radiometric methods are based, we find:
1. It is assumed that the earth began as a spinning blob of hot liquid that cooled to form the original rock surface. It is further assumed that, because of the immense span of time during which erosion and rebuilding are believed to have taken place, none of the original crustal materials are now available for study.
2. It is assumed that the crystals that are selected for radiometric age determination have been formed either by growing from hot liquid, that is, igneous rock, or by metamorphosis. Metamorphosis is a process in which crystallization occurs in sedimentary rock and is believed to take place by sustained high pressure and possible high temperatures but without melting the rock.
3. Once the crystal has formed, it is assumed that it is a closed system, that is, no "parent" or "daughter" elements enter or leave the crystal lattice; the only change that takes place is assumed to be decay of the unstable "parent" with time and consequent increase of the stable "daughter" element.
4. When discordant results are obtained from processes operating within the same crystal, it is assumed that there has been loss or addition of the "daughter" product. That is, selective loss of either lead 206 or argon 40 is claimed when the sample appears too young and selective addition or contamination when it appears too old.
5. Contamination of the crystal during its formation by extraneous "daughter" elements has to be taken into account, and it is assumed that the various isotope ratios of the contaminating element were the same at the time of crystal formation as they are today.
6. It is assumed that the decay "constant", determined over a two-or three-day period and mathematically related to the rate of decay expressed as half-life, has remained unchanged throughout the entire age of the mineral sample.
Relevant to the first assumption, it is worth recalling that while Holmes (1956) has estimated the age of the earth to be 4.5 billion years, no terrestrial rocks of this age have ever been reported, since it is assumed that all the original crustal material had been eroded then redeposited as sedimentary rock. The oldest rocks on earth have a reported age of 3.8 billion years. However, it was realized that the moon would have crusted over at about the same time as the earth; since there is no wind or water to cause erosion, it was believed moon rocks would provide a direct radiometric age for the earth. Sure enough, after retrieval of the moon rock samples in the Apollo program, Holmes' estimation was claimed to be exactly confirmed, and the age of the earth confidently stated in the popular press[19] and textbooks[20] to be 4.5 billion years (Eldredge 1982, 104; Taylor 1975). However, the official reports and scientific journals, in which actual results of the radiometric determinations were given, showed that the ages of the moon-rock samples varied between 2 and 28 billion years (Whitcombe and DeYoung 1978).[21] Quite evidently, the data for public consumption had been selected to confirm the theory.
The last assumption (6) is, strictly speaking, an extrapolation of data
on a huge scale, far beyond what is considered good practice under any
other circumstance. We are reminded that the atomic decay is assumed to
be at a constant rate, so that the data collected over a few days and checked
infrequently during this century has been applied to billions of years.
Some are beginning to question this whole line of thinking, and Professor
Dudley, writing in 1975, has been particularly outspoken: "These equations
resulted initially from studies done with crude instruments some 70 years
ago. Bluntly they are incorrect, nonetheless appear in our latest textbooks
to compound the errors of past generations. This in spite of more recent
evidence" (Dudley 1975, 2).[22
]
At the root of this complaint is the constancy of the decay constant.
A Closer Look at the Universal Constants
The mechanics of radioactive decay are dealt with at length and in mathematical detail by specialist books on the subject, and it would not be appropriate to attempt to cover this topic here. Suffice it to say that radioactive decay depends on the probability of escape of certain particles from their orbit in the unstable atom. The decay rate is directly proportional to the speed of travel of the particles in their atomic orbit, and this speed is, in turn, directly proportional to the speed of light. It may seem odd that the speed of light is related to atomic phenomena, but it does turn up in a number of seemingly unlikely places as one of the universal constants. For instance, in the familiar expression E=mc2 , we find that the velocity of light, c, is related to the mass, m, and the energy, E.
There are other parameters with which physics is concerned and which are related to the speed, or velocity, of light. The permittivity of free space, for example, is one of the constants that relate electrical force to electrical charge, while there is another constant that relates electrical charge to the mass of the electron. However, the meaning of all these rather esoteric terms is not really important in this present context, and it need only be said that they are all interrelated as universal constants. It was pointed out earlier in this chapter that it is a natural consequence of the uniformitarian mind-set to assume that the universal constants are, in fact, constant and have been throughout all time. Once again, we confront the unknowable and unprovable in dealing with events in the past, in this case dynamic relationships in natural processes.
The second law of thermodynamics points out that the universe is "running
down", and, in familiar examples, we see the outworkings of this law in
the death of living organisms and in the wear and decay of inanimate things,
such as the family car. This is accepted today as a self-evident and universal
law. But when it was first proposed by Kelvin and others in the last century,
it met with great opposition from Darwin's followers. If accepted, they
would be faced with the difficulty of showing how a chance process (natural
selection) could build up the elements from the simple to the complex,
that is, from nonlife to life. Nevertheless, the illogical has occurred
and both the second law and the theory of evolution exist side by side
today. From the universal nature of the second law, it might then be wondered
if the universal constants are not also subject to the same law, bearing
in mind that they were only assumed to be constants in the first place.
In other words, it is legitimate to ask whether the speed of light could
have been greater in the past, or the related question of whether the nuclear
decay processes have been slowing down with time, so that the half-lives
in the past were much shorter. There may never be proof either of constancy
or change with time, but it is surely not in the true spirit of scientific
inquiry to make the dogmatic assertion that the values have always been
constant when no one measured these parameters in the remote past. In fact,
there is some evidence to suggest that the universal constants have been
changing with time and in the direction that might be expected from the
second law of thermodynamics.
Is the Velocity of Light Constant?
The Danish astronomer Roemer made the first determination of the velocity of light in 1675 by observing the eclipses of Jupiter's moons (Velocity of Light 300 years ago; Hynek 1983).[23] Using the present-day values for the earth's orbital diameter about the sun, recalculation of Roemer's data shows that the velocity of light then would have been 301,300 kilometers per second (Goldstein et al. 1973).[24] Since that date, more than forty determinations have been made with increasing precision, and the accepted value today is 299,792.44 kilometers (185,871 miles) per second. However, there have been some unexpected disagreements, leading several workers to question if the velocity of light is actually a constant (Strong 1975; Tolles 1980).[25] Rush, writing in 1955, claims that it had increased by 16 kilometers per second during the previous decade. Setterfield, meanwhile, maintains that when the data for the entire 300-year period is subjected to analysis, there has been a definite decrease (Steidl 1982).[26] For those of sufficient curiosity, the values reported for the past three centuries are given in Appendix D.
The immediate reaction to an apparent violation of a universal constant is likely to be either outright disbelief or the cry that experimental techniques have improved and we now have more reliable values. The possibility of nonconstancy cannot be dismissed so readily, however, and for a number of good reasons. First, a universal law has not been violated; it is simply being proposed that the original assumptions were incorrect. Second, as more and better data accumulate, it is becoming evident that many parameters traditionally accepted as universal constants are changing; Wesson (1979, 115) and others have made this same observation (Catacosinos 1975; Dostal et al. 1977). Third, and most important, when taken all together, those universal constants for which there is sufficient data do show a definite change in both magnitude and direction, consistent with what would be expected from the second law of thermodynamics. The values of some of these related universal constants are listed in Appendices E to H, and in each case the gradual change of the "constant" with time may be clearly seen. The author is indebted to Barry Setterfield for these insights and painstaking gathering together of all the information (pers. com. 1983).
If, as it appears, these universal constants have changed with time,
then the velocity of light and the nuclear decay constants will also have
changed, since they are related. Moreover, from the direction of change
indicated by the results, the velocity of light would have been greater
in the past. This raises the possibility that the time taken for the light
from the furthest star to reach earth may have been, for example, a few
years rather than, as in current thinking, millenia of years. The distances
may be great but the vast spans of time are based on an assumption. The
subject has been questioned before; for example, astronomers Moon and Spencer
(1953) have taken an entirely different approach and concluded that light
from the most distant stars may have reached us in only fifteen years.[27]
Even to countenance the possibility that the velocity of light has not
been subject to the uniformitarian dogma requires a certain fortitude of
character, because the whole of cosmology is dependent on this assumption,
and it would mean, for example, that the age of the universe would require
drastic revision -- downwards.
Are Decay Constants Constant?
If all the other universal constants have changed with time, then the nuclear decay constants must also have changed, since they are related, and we would expect to find shorter half-lives in the past. Unfortunately, for a number of reasons there is very little direct evidence. First, the early measurements that were made more than seventy years ago were of rather low precision. In more recent years, the counting technique has greatly improved, with the result that there is now much greater precision; it is somewhat meaningless, therefore, to compare these results. Second, by calling the nuclear decay parameter a "constant", there is little expectation of a change once a value has been agreed on. Changes that may have occurred could, thereby, have easily been overlooked. From the published half-lives of some of the long-lived radioactive elements, it seems that there is a precision of about one part in a thousand, while there are two cases reported where the half-life is increasing with time. The half-life of protoactinium 231 has increased from 32,000 years in 1950 to 34,300 years in 1962, and the half-life of radium 223 has increased from 11.2 days to 11.68 days over the same period of time.
Although the proposal that nuclear decay has changed over thousands of years cannot be proven, neither can the assumption that it has been constant, and it would seem only fair to consider what a decreasing decay rate would mean. With an increasing rate into the past, this would mean that the half-lives would get progressively shorter further back in time, so that most of the decay would have taken place shortly after the beginning. This would explain why the naturally occurring radioactive elements all have relatively long half-lives today. At the same time it explains the absence of those elements with the shorter half-lives, since these would have long ago decayed past their ten half-life period and not now be detectable.
It was previously mentioned in this chapter that radioactive dates generally get older with increasing depth in the rock strata, and this is taken to be one of the prime pieces of evidence for evolution over vast periods of time. If the sediments were the result of a worldwide flood, however, then the lava flows that were intermixed with the sediments would have been deposited over a brief historical period -- a year or so, for example. If this proposal is correct, then most of the radioactive decay took place in the first few days or weeks, and the record preserved in the rock immediately after it became solid. Lava beds that differed in age by weeks or months of each other would then appear to differ by millions of years.
Perhaps it is now possible to see how two observers could come to entirely different conclusions by approaching the same evidence with different preconceptions. The first observer, having been schooled to think in terms of Lyell's uniformitarianism, would assume that nuclear decay rates were constant throughout all time and from radiometric measurements determine that a certain fossil was, for example, 100 million years old. This value would be accepted by his peers if it conformed to the expected age for that particular fossil creature. The second observer might assume that nuclear decay had been subject to the second law of thermodynamics, by reason of changing permittivity, for example, and the decay rate itself had decreased with time. His mathematical interpretation of the same radiometric measurements for the same fossil would then yield a value of only a few thousand years, and this great difference in age, it will be recalled, came about by the initial assumption on the part of each observer.
# # #
This chapter has attempted to present, in sufficient detail, the assumptions
underlying radiometric dating, in order that the reader may begin to judge
for himself the claims for an old earth made on the basis of this method.
The following chapter presents some further aspects related to radiometric
dating that should be considered, together with a number of quite unrelated
processes, all of which indicate a youthful earth.
|
|
| << PREV |
|